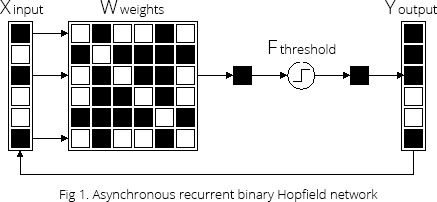
Modern neural networks is just playing with matrices. So in a few words, Hopfield recurrent artificial neural network shown in Fig 1 is not an exception and is a customizable matrix of weights which is used to find the local minimum (recognize a pattern). The Hopfield model accounts for associative memory through the incorporation of memory vectors and is commonly used for pattern classification.
Contents
- Quick reference
- Theory
- Algorithm
- Matlab code
- C code
- Application examples
- Cross associations
- Pros and cons
Quick reference
A Hopfield network is a form of recurrent artificial neural network popularized by John Hopfield in 1982 but described earlier by Little in 1974. Hopfield nets serve as content-addressable memory systems with binary threshold nodes. They are guaranteed to converge to a local minimum, but convergence to a false pattern (wrong local minimum) rather than the stored pattern (expected local minimum) can occur. Hopfield networks also provide a model for understanding human memory. More details – https://en.wikipedia.org/wiki/Hopfield_network
Theory
A Hopfield neural network is a particular case of a Little neural network. So it will be interesting to learn a Little neural network after.
A Hopfield neural network is a recurrent neural network what means the output of one full direct operation is the input of the following network operations, as shown in Fig 1.
Associative memory
It has been proved that Hopfield network is resistant. In general, it can be more than one fixed point. What fixed point will network converge to, depends on the starting point chosen for the initial iteration.
The fixed points called attractors. The set of points (vectors) that are attracted to a particular attractor in the network of iterations, called “attraction area” of the attractor. The set of fixed points of the Hopfield network – is its memory. In this case, the network can act as an associative memory. Those input vectors that fall within the sphere of attraction of a separate attractor, are related (associated) with them.
For example, the attractor may be some desired pattern. Attraction area may consist of noisy or incomplete versions of this pattern. It’s hoped that the pattern that vaguely resembles the desired pattern will be recalled and associated properly by a network.
Binary model
Fig 1 shows a binary Hopfield network, binary means +1 or -1. Any black and white picture could be represented as sequance of black (+1) and white (-1) pixels which constitute the input vector. The input and output vectors consist of “-1” and “+1” (instead of “-1” can be used “0”) has a symmetric weight matrix composed of integers with zero diagonal ![]() . Zero diagonal is a recommended condition for the convergence, but not the required one.
. Zero diagonal is a recommended condition for the convergence, but not the required one.
Weight matrix
The weight matrix differentiates the behavior of a one Hopfield network from another, so the question arises: “How to determine the weight matrix?“.
The answer – it’s necessary to specify a certain weight vectors, which are called instances. It is hoped that these instances are fixed points of the resulting network Hopfield. Although this is not always the case. In order to instances were attractors, it’s necessary to set the weight matrix as follows:
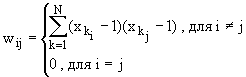 (1)
(1)where N – the number of specified instances, and ![]() – k-th instance.
– k-th instance.
If instances of the vectors form a set of orthogonal vectors, it is possible to ensure that if the weight matrix is chosen as indicated above, each copy of the vector is a fixed point. However, in general, in order to instances lead to fixed points, orthogonality is not required.
Energy
Hopfield nets have a scalar value associated with each state of the network referred to as the “energy”, E, of the network, where:
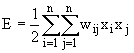 (2)
(2)This value is called the “energy” because the definition ensures that when points are randomly chosen to update, the energy E will either lower in value or stay the same. Furthermore, under repeated updating, the network will eventually converge to a state which is a local minimum in the energy function.
Asynchronous correction
- Asynchronous: Only one unit is updated at a time. This unit can be picked at random, or a pre-defined order can be imposed from the very beginning.
- Synchronous: All units are updated at the same time. This requires a central clock to the system in order to maintain synchronization. This method is less realistic since biological or physical systems lack a global clock that keeps track of time.
The input vector X is multiplied by the weight matrix using the normal matrix-vector multiplication. However, only one component of the output vector is used at each iteration. This procedure is known as “asynchronous correction“. This component, which may be randomly selected is applied to the threshold element whose output -1 or 1. The corresponding component of the input vector is replaced by the value, and thus forms the input vector for the next iteration. The process continues as long as the input and output vectors do not become the same (i.e., until a fixed point is reached)
Synchronous correction – means that the whole output vector is used at each iteration. Note that asynchronous correction is much more precise then synchronous correction, but it requires more computing power. Nowadays only asynchronous correction is commonly used.
Asynchronous correction and zeros on the diagonal of weights matrix W ensure that the energy function (2) will decrease with each iteration. Asynchronous correction – it’s particularly important to ensure convergence to the fixed point. If we would work with synchronous correction and assume that the whole vector is adjusted at each iteration, the network can be with periodic cycles like terminal states of attractors, and not with the fixed points.
Algorithm
- Calculate the weight matrix W using the formula (1).
- Calculate the output vector components, j = 1,2, .., n, using the formula below:
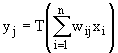 (3)
(3)
where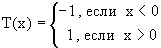
- Perform the asynchronous correction:
- Repeat steps 2-3 for as long as the vector
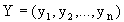 is no longer changed. Each step reduces the amount of energy ties:
is no longer changed. Each step reduces the amount of energy ties: 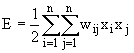 (2)
(2)
Matlab code
The Matlab has a newhop() function which can do the job for us, but we would like to develop the code for ourselves:
| %{ Author: Alex Bod | |
| % Website: https://www.alexbod.com | |
| % Details: https://www.alexbod.com/hopfield-network/ | |
| % License: The GNU General Public License, version 2 | |
| % hopfield.m: Hopfield network in Matlab | |
| %} | |
| % Input data for learning | |
| x = [' OO '; ... | |
| ' OO '; ... | |
| ' OOOO '; ... | |
| ' O O '; ... | |
| ' OO OO '; ... | |
| ' O O '; ... | |
| ' OOOOOOOO '; ... | |
| ' OOOOOOOO '; ... | |
| 'OO OO'; ... | |
| 'OO OO']; | |
| x(:, :, 2) = ... | |
| ['OOOOOO '; ... | |
| 'OOOOOOO '; ... | |
| 'OO OO '; ... | |
| 'OOOOOOO '; ... | |
| 'OOOOOOO '; ... | |
| 'OO OOO '; ... | |
| 'OO OO '; ... | |
| 'OO OOO '; ... | |
| 'OOOOOOO '; ... | |
| 'OOOOOO ']; | |
| x(:, :, 3) = ... | |
| ['OOOOOOOOOO'; ... | |
| 'OOOOOOOOOO'; ... | |
| 'OO OO'; ... | |
| 'OO '; ... | |
| 'OO '; ... | |
| 'OO '; ... | |
| 'OO '; ... | |
| 'OO OO'; ... | |
| 'OOOOOOOOOO'; ... | |
| 'OOOOOOOOOO']; | |
| x(:, :, 4) = ... | |
| ['OO OO'; ... | |
| 'OO OO'; ... | |
| 'OO OO'; ... | |
| 'OO OO'; ... | |
| 'OOOOOOOOOO'; ... | |
| 'OOOOOOOOOO'; ... | |
| 'OO OO'; ... | |
| 'OO OO'; ... | |
| 'OO OO'; ... | |
| 'OO OO']; | |
| % Input data for recognition | |
| y = [' OO '; ... | |
| ' OO '; ... | |
| ' OOOO '; ... | |
| ' O OO '; ... | |
| ' OO OOO '; ... | |
| ' O OO '; ... | |
| ' OOOOOOOO '; ... | |
| ' OOOOOOOO '; ... | |
| 'OO OO'; ... | |
| 'OO OO']; | |
| y(:, :, 2) = ... | |
| ['OOOOOOO '; ... | |
| 'OOOOOOOOO '; ... | |
| 'OO OOOO '; ... | |
| 'OOOOOOOOO '; ... | |
| 'OOOOOOO '; ... | |
| 'OO OOO '; ... | |
| 'OO OO '; ... | |
| 'OO OOO '; ... | |
| 'OOOOOOO '; ... | |
| 'OOOOOOOO ']; | |
| y(:, :, 3) = ... | |
| ['OOOOOOOOOO'; ... | |
| 'OOOOOOOOOO'; ... | |
| 'OO OO'; ... | |
| 'OO '; ... | |
| 'OOOOOO '; ... | |
| 'OO OOO '; ... | |
| 'OO '; ... | |
| 'OO OO'; ... | |
| 'OOOOOOOOOO'; ... | |
| 'OOOOOOOOOO']; | |
| y(:, :, 4) = ... | |
| ['OO OO'; ... | |
| 'OO OO'; ... | |
| 'OO OOOO OO'; ... | |
| 'OO OO'; ... | |
| 'OOOOOOOOOO'; ... | |
| 'OOOOOOOOOO'; ... | |
| 'OO OO'; ... | |
| 'OO OOOO OO'; ... | |
| 'OO OO'; ... | |
| 'OO OO']; | |
| % Input data for learning | |
| input = zeros(size(x,3),100); | |
| % Input data for recognition | |
| notcorrect = zeros(size(y,3),100); | |
| % Make x input data binary | |
| for n = 1:1:size(x,3) | |
| for i = 1:1:10 | |
| for j = 1:1:10 | |
| if x(i,j,n) == 'O' | |
| input(n,(i-1)*10+j) = 1; | |
| else | |
| input(n,(i-1)*10+j) = -1; | |
| end | |
| end | |
| end | |
| end | |
| % Make y input data binary | |
| for n = 1:1:size(y,3) | |
| for i = 1:1:10 | |
| for j = 1:1:10 | |
| if y(i,j,n) == 'O' | |
| notcorrect(n,(i-1)*10+j) = 1; | |
| else | |
| notcorrect(n,(i-1)*10+j) = -1; | |
| end | |
| end | |
| end | |
| end | |
| % Initialize weight matrix | |
| W = zeros(size(x,1),size(x,2)); | |
| % Calculate weight matrix = learning | |
| for i = 1:1:size(x,1)*size(x,2) | |
| for j = 1:1:100 | |
| weight = 0; | |
| if (i ~= j) | |
| for n = 1:1:size(x,3) | |
| weight = input(n,i) .* input(n,j) + weight; | |
| end | |
| end | |
| W(i,j) = weight; | |
| end | |
| end | |
| % Recognition | |
| for n = 1:1:size(y,3) | |
| iteration = 0; | |
| iterationOfLastChange = 0; | |
| propagateUnit = 0; | |
| flag = true; | |
| while flag | |
| % Counter | |
| iteration = iteration + 1; | |
| % Generate random element for the asynchronous correction | |
| i = randi([1 size(x,1)*size(x,2)],1,1); | |
| sum = 0; | |
| for j = 1:1:size(x,1)*size(x,2) | |
| sum = sum + W(i, j) * notcorrect(n,j); | |
| end | |
| % Therehold | |
| out = 0; | |
| changed = 0; | |
| if (sum ~= 0) | |
| if (sum < 0) | |
| out = -1; | |
| end | |
| if (sum > 0) | |
| out = +1; | |
| end | |
| if (out ~= notcorrect(n, i)) | |
| changed = 1; | |
| notcorrect(n,i) = out; | |
| end | |
| end | |
| % Main condition | |
| if (changed == 1) | |
| iterationOfLastChange = iteration; | |
| end | |
| % Break condition | |
| if (iteration - iterationOfLastChange > 1000) | |
| flag = false; | |
| end | |
| end | |
| % Show the initial not correct input | |
| for i = 1:1:size(y,1) | |
| for j = 1:1:size(y,2) | |
| fprintf('%s', y(i,j,n)); | |
| end | |
| fprintf('\n'); | |
| end | |
| fprintf('\n\n'); | |
| % Show the recognized pattern | |
| for i = 1:1:size(x,1)*size(x,2) | |
| if (rem(i-1, 10) == 0) && (i ~= 1) | |
| fprintf('\n'); | |
| end | |
| if notcorrect(n,i) == 1 | |
| fprintf('O'); | |
| elseif notcorrect(n,i) == -1 | |
| fprintf(' '); | |
| else | |
| fprintf('!'); | |
| end | |
| end | |
| fprintf('\n\n----------\n\n'); | |
| end | |
Clone it from the Github
C code
| /* Author: Alex Bod | |
| * Website: https://www.alexbod.com | |
| * Details: https://www.alexbod.com/hopfield-network/ | |
| * License: The GNU General Public License, version 2 | |
| * hopfield.c: Hopfield network in C | |
| */ | |
| #include <stdlib.h> | |
| #include <stdio.h> | |
| #include <unistd.h> | |
| /* Convert points */ | |
| #define ZERO_OR_ONE(x) ((x)==-1 ? 0 : 1) | |
| #define BINARY(x) ((x)== 0 ? -1 : 1) | |
| #define NUMBER_OF_VECTORS 4 | |
| #define X 10 | |
| #define Y 10 | |
| #define AREA (X * Y) | |
| /* Network struct */ | |
| typedef struct { | |
| int points; | |
| int* output; | |
| int* threshold; | |
| int** weight; | |
| } net; | |
| /* Input data for learning */ | |
| char x[NUMBER_OF_VECTORS][Y][X] = | |
| {{ " OO ", | |
| " OO ", | |
| " OOOO ", | |
| " O O ", | |
| " OO OO ", | |
| " O O ", | |
| " OOOOOOOO ", | |
| " OOOOOOOO ", | |
| "OO OO", | |
| "OO OO"}, | |
| {"OOOOOO ", | |
| "OOOOOOO ", | |
| "OO OO ", | |
| "OOOOOOO ", | |
| "OOOOOOO ", | |
| "OO OOO ", | |
| "OO OO ", | |
| "OO OOO ", | |
| "OOOOOOO ", | |
| "OOOOOO "}, | |
| {"OOOOOOOOOO", | |
| "OOOOOOOOOO", | |
| "OO OO", | |
| "OO ", | |
| "OO ", | |
| "OO ", | |
| "OO ", | |
| "OO OO", | |
| "OOOOOOOOOO", | |
| "OOOOOOOOOO"}, | |
| {"OO OO", | |
| "OO OO", | |
| "OO OO", | |
| "OO OO", | |
| "OOOOOOOOOO", | |
| "OOOOOOOOOO", | |
| "OO OO", | |
| "OO OO", | |
| "OO OO", | |
| "OO OO"}}; | |
| /* Input data for recognition */ | |
| char y[NUMBER_OF_VECTORS][Y][X] = | |
| {{" OO ", | |
| " OO ", | |
| " OOOO ", | |
| " O OO ", | |
| " OO OOO ", | |
| " O OO ", | |
| " OOOOOOOO ", | |
| " OOOOOOOO ", | |
| "OO OO", | |
| "OO OO"}, | |
| {"OOOOOOO ", | |
| "OOOOOOOOO ", | |
| "OO OOOO ", | |
| "OOOOOOOOO ", | |
| "OOOOOOO ", | |
| "OO OOO ", | |
| "OO OO ", | |
| "OO OOO ", | |
| "OOOOOOO ", | |
| "OOOOOOOO "}, | |
| {"OOOOOOOOOO", | |
| "OOOOOOOOOO", | |
| "OO OO", | |
| "OO ", | |
| "OOOOOO ", | |
| "OO OOO ", | |
| "OO ", | |
| "OO OO", | |
| "OOOOOOOOOO", | |
| "OOOOOOOOOO"}, | |
| {"OO OO", | |
| "OO OO", | |
| "OO OOOO OO", | |
| "OO OO", | |
| "OOOOOOOOOO", | |
| "OOOOOOOOOO", | |
| "OO OO", | |
| "OO OOOO OO", | |
| "OO OO", | |
| "OO OO"}}; | |
| /* Input data for learning */ | |
| int input[NUMBER_OF_VECTORS][AREA]; | |
| /* Input data for recognition */ | |
| int notcorrect[NUMBER_OF_VECTORS][AREA]; | |
| /* Print the result */ | |
| void printNet(net* network) | |
| { | |
| int i,j; | |
| for (i=0; i<Y; i++) { | |
| for (j=0; j<X; j++) { | |
| printf("%c", ZERO_OR_ONE(network->output[i*X+j]) ? 'O' : ' '); | |
| } | |
| printf("\n"); | |
| } | |
| printf("\n"); | |
| } | |
| /* Create the net */ | |
| void createNet(net* network) | |
| { | |
| int i; | |
| network->points = AREA; /* Number of points = net area */ | |
| network->output = (int*)calloc(AREA, sizeof(int)); | |
| network->threshold = (int*)calloc(AREA, sizeof(int)); | |
| network->weight = (int**)calloc(AREA, sizeof(int*)); | |
| /* Fill thresholds with zeros and allocating memory for weight matrix */ | |
| for (i=0; i<AREA; i++) { | |
| network->threshold[i] = 0; | |
| network->weight[i] = (int*)calloc(AREA, sizeof(int)); | |
| } | |
| } | |
| /* Convert points of 'O' to the binary -1 or +1 */ | |
| void pointstoBinary(net* network) | |
| { | |
| int n,i,j; | |
| for (n=0; n<NUMBER_OF_VECTORS; n++) { | |
| for (i=0; i<Y; i++) { | |
| for (j=0; j<X; j++) { | |
| /* Make points binary and convert 3d matrix to 2d */ | |
| input[n][i*X+j] = BINARY(x[n][i][j] == 'O'); | |
| notcorrect[n][i*X+j] = BINARY(y[n][i][j] == 'O'); | |
| } | |
| } | |
| } | |
| } | |
| /* Calculate the weight matrix = learning */ | |
| void calculateWeights(net* network) | |
| { | |
| int i,j,n; | |
| int weight; | |
| for (i=0; i<network->points; i++) { | |
| for (j=0; j<network->points; j++) { | |
| weight = 0; | |
| if (i!=j) { | |
| for (n=0; n<NUMBER_OF_VECTORS; n++) { | |
| /* Main formula for calculating weight matrix */ | |
| weight += input[n][i] * input[n][j]; | |
| } | |
| } | |
| /* Fill the weight matrix */ | |
| network->weight[i][j] = weight; | |
| } | |
| } | |
| } | |
| /* Set the input vector to the Net->output */ | |
| void setInput(net* network, int* input) | |
| { | |
| int i; | |
| for (i=0; i<network->points; i++) { | |
| network->output[i] = input[i]; | |
| } | |
| printNet(network); | |
| } | |
| /* Set the Net->output to the output vector */ | |
| void getOutput(net* network, int* output) | |
| { | |
| int i; | |
| for (i=0; i<network->points; i++) { | |
| output[i] = network->output[i]; | |
| } | |
| printNet(network); | |
| printf("----------\n\na"); | |
| } | |
| /* Next iteration to find the local minimum = recognized pattern */ | |
| int nextIteration(net* network, int i) | |
| { | |
| int j; | |
| int sum, out; | |
| int changed; | |
| changed = 0; | |
| sum = 0; | |
| for (j=0; j<network->points; j++) { | |
| sum += network->weight[i][j] * network->output[j]; | |
| } | |
| if (sum != network->threshold[i]) { | |
| if (sum < network->threshold[i]) out = -1; | |
| if (sum > network->threshold[i]) out = 1; | |
| if (out != network->output[i]) { | |
| changed = 1; | |
| network->output[i] = out; | |
| } | |
| } | |
| return changed; | |
| } | |
| /* Asynchronous correction */ | |
| void asynCor(net* network) | |
| { | |
| int iteration; | |
| int iterationofLastChange; | |
| iteration = 0; | |
| iterationofLastChange = 0; | |
| do { | |
| iteration++; | |
| /* Every time take random element for the correction */ | |
| if (nextIteration(network, rand() % (network->points))) | |
| iterationofLastChange = iteration; | |
| } while (iteration-iterationofLastChange < 10*network->points); | |
| } | |
| /* Find the local minimum = recognizing the pattern */ | |
| void findLocalMinimum(net* network, int* input) | |
| { | |
| int output[AREA]; | |
| /* Print not correct input for recognizing */ | |
| setInput(network, input); | |
| /* Asynchronous correction */ | |
| asynCor(network); | |
| /* Print recognized output */ | |
| getOutput(network, output); | |
| } | |
| void main() | |
| { | |
| net network; | |
| int n; | |
| /* Allocate memory and create the net */ | |
| createNet(&network); | |
| /* Make the points matrix binary */ | |
| pointstoBinary(&network); | |
| /* Calculate the weight matrix */ | |
| calculateWeights(&network); | |
| /* Find the local minimum = recognizing the pattern */ | |
| for (n=0; n<NUMBER_OF_VECTORS; n++) { | |
| findLocalMinimum(&network, notcorrect[n]); | |
| } | |
| } |
Clone it from the Github
Application examples
Initial patterns
|
OO |
OOOOOO |
OOOOOOOOOO |
OOOO |
Noise test
| The test pattern | Noise percternentage | Type of a distorted pattern | The result of recognition |
|
OO |
10% |
OO |
OO |
| 20% |
OOOO |
OO |
|
| 30% |
OOOO |
OO |
|
| 40% |
OOOOOOO |
OO |
|
| 50% |
OOOOOOO |
OO |
|
| 60% |
OOOOOOO |
OOOOOOOOOO |
|
| 70% |
OOOOOOOOOO |
OOOOOOOO |
|
| 80% |
OOOOOOOO |
OOOOOOOO |
|
| 90% |
OOOOOOOO |
OOOOOOOO |
|
| 100% |
OOOOOOOO |
OOOOOOOO |
The test above gave very accurate recognition result even if the noise level is greater than 50%, and even a man is hard to recognize.
Rotate test
| The test pattern | Rotate angle | Type of a distorted pattern | The result of recognition |
|
OOOO |
30° |
OO |
OOOO |
| 40° |
O |
|
|
| 90° |
OOOOOOOOOO |
OOOOOOOOOO |
The test above shown inability to recognize a pattern when it’s rotated, especially when the rotational angle is 90°. The first pattern is recognized because it looks like the initial pattern with the noise.
Cross associations
Let’s complicate the task and train the network to recognize one more pattern:
OOOOOOOOOO
OOOOOOOOOO
OOOO
OO
OO
OOOOOO
OOOOOO
OOOO
OOOOOOOOOO
OOOOOOOOOO
The letter “G” is very similar to already existing in the network memory letter “C”. Now the network can not recognize any of these letters, even in the undistorted state. Instead of correctly recognized letters it produces something in between (for the distortion of the pattern from 0 to 50%):
| The test pattern | The result of recognition |
|
OOOOOOOOOO |
OOOOOOOOOO |
|
OOOOOOOOOO |
OOOOOOOOOO |
It looks a little bit like an every letter “G”, “C”, and it’s not a correct interpretation of any of them.
Furthermore this disturbance affected other patterns with different recognizing parameters.
| The test pattern | The result of recognition |
|
OOOOOOO |
OOOOOOOOOO |
But letter “A” without distortions is recognized correctly.
| The test pattern | The result of recognition |
|
OO |
OO |
The described behavior of the neural network is known as the effect of “Cross associations”.
Pros and cons
Pros
- Accurate recognition even if the noise level is greater than 50%, and even a man is hard to recognize.
Cons
- Presence of the cross associations when multiple patterns is similar to each other (such as in the experimentation with the letters “G” and “C”).
- Capacity limits of the the number of stored memory attractor is just (0.3/0.4)*n, where n – the dimension of the weight matrix W.
- Inability to recognize a pattern when it’s rotated.
These cons substantially limits the practical use of the Hopfield network but I believe that with a little revision the situation can be fixed.
P.S. If you want to learn neural networks, learn mathematics, especially matrices and their operations.